Tweak3D.net - Bump Mapping: How It Works

Posted: June 11, 2000
Written by: Tuan "Solace" Nguyen

Emboss Bump Mapping (cont.)

Lets do an example on a one dimensional bump map for simplicity's sake. The map only varies as a function of s. Assuming that the height values of the bump map can be represented as a height function f(s), then the three step process above would be like doing the following: f(s) - f(s + shift). If the shift was by one texel in s, you would have: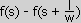

, where w is the width of the texture in texels and l is the length. This is a different form of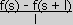

which is just the basic derivative formula. So shifting and subtracting results in the first derivative of f(s), f'(s) -- f-prime at s.

In the two dimensional case, the height function is f(s,t), and shifting and subtracting creates a directional derivative of f(s,t). This technique is used to create embossed images.

What does this all mean? All this does is simulate a texture's height in reference to a light source. If one part of the object is closer to the light, it will be lit up more brightly. Now if you apply those simulations to a flat texture and point out where light should hit and not, then you can simulate 3D roughness on the flat plane without adding more geometric detail -- actual polygonal bumps.

Limitations to Embossing:

Bump Map Sampling: The bump map height function is not continuous, but is rendered right into the texture, making it permanent. The resolution of the texture affects how accurately the bump map is rendered. Increasing the size of the bump map texture (the duplicate of the actual texture map) can improve rendering of extreme heights in the texture.

Texture Resolution: The shifting and subtraction steps produce the opposite direction map. Since this is a forward differencing technique, the highest height component of the bump map increases as the shift to the bump map is made smaller. As the shift reduces in size, the texture coordinate precision must increase in accuracy. The map shift can become smaller than the texture filtering implementation can handle, leading to texture noise and aliases effects making the final image seem ripped or broken and can turn out perceptively incorrect.

Surface Curvature: The height coordinates are different for each point on a curved surface. This technique approximates this by interpolating the height transforms for each vertex on the polygon being bump mapped. For polygons with very different vertex normals, the interpolation will not work because of major differences. It's like being asked to guess what a secret is without a clue. If you have more clues, you will be able to guess more accurately.

Maximum Bump Map Slope: The bump map perpendiculars used in this technique are good approximations if the bump map slope is small. If there are steep tangents in the bump map, the assumption that the bump perpendicular length is equal to 1 becomes inaccurate, and the highlights appear too bright because it assumes that that point on the bump is very close to the light source, which it isn't. It is merely much more higher than the other bumps. Embossing requires that all bumps on a particular surface be the same.

The above diagram illustrates that the embossing effect no longer works when the light source moves past a certain degree of incident. For the lighting to work, the reflected angle must remain acute or smaller than 90 degrees from the normal.

Next Page